Sut i ddefnyddio a sefydlu cyfartaleddau symudol wrth fasnachu

Yn ystod esblygiad masnachu dadansoddi technegol, mae llawer o offer wedi dod i’r amlwg. Ond ymhlith y dangosyddion mwyaf syml, defnyddiol, diogel a chyffredin mewn masnachu, mae cyfartaleddau symudol yn cael eu gwahaniaethu. Mae’r canlynol yn disgrifio eu rheidrwydd wrth fasnachu a nodweddion defnyddio gwahanol fathau o gyfartaleddau symudol mewn strategaeth fasnachu.

Beth yw cyfartaleddau symudol wrth fasnachu

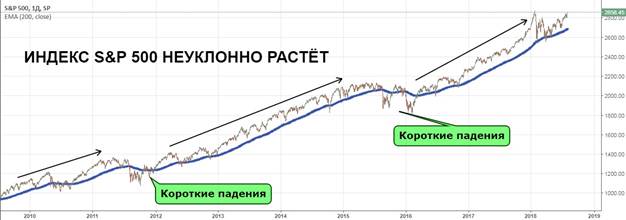
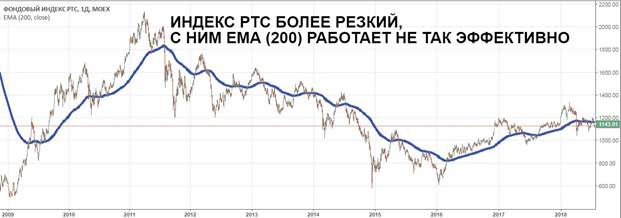
Symud Cyfartaledd, neu fel y’i gelwir hefyd, Symud Cyfartaledd (MA) yn ddangosydd masnachu sy’n dilyn y symudiad pris. Ei ddiben yw sefydlu cyfeiriad y duedd a’r posibilrwydd o’i lyfnhau. Wrth gyfrifo’r cyfartaledd symudol, mae arbenigwyr yn dewis cyfartaledd pris offeryn penodol am gyfnod penodol.
Y cyfnod yw prif ddangosydd y dangosydd cyfartaledd symudol, un o’r mathau. Mae lefel llyfnder llinell y dangosydd yn dibynnu ar ei werth. Mae cyfnodau bach yn fwy priodol mewn cyfnodau amser isel. Maent yn caniatáu hyd yn oed masnachwr dibrofiad i ymateb yn gyflym i symudiadau pris.

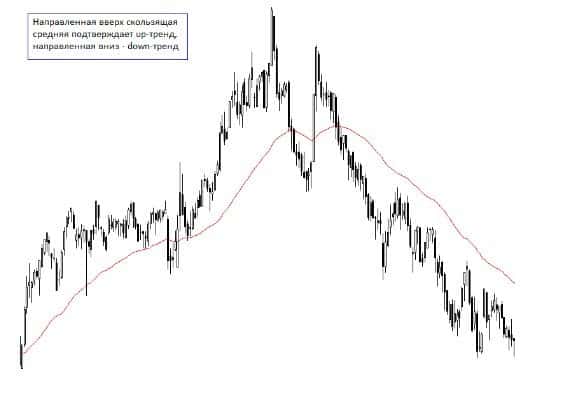
Fodd bynnag, nid yw signalau ffug (weithiau mewn niferoedd mawr) yn cael eu diystyru.

Os cymhwysir cyfnod rhy hir, mae’n bwysig bod yn ymwybodol y gall gael ei ohirio’n ddramatig. Am yr un rheswm, bydd y system yn dangos hanes sydd wedi dyddio. Defnyddir cyfnodau mawr yn aml ar gyfer cefnogaeth neu wrthwynebiad hirdymor.

Prif fathau o Gyfartaledd Symudol a’u disgrifiad

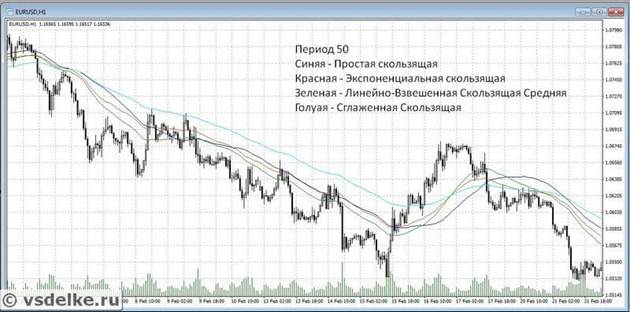
Mae 4 prif fath o ddangosydd MA. Wrth weithredu dadansoddiad technegol y farchnad fuddsoddi, defnyddir cyfartaledd symudol syml, esbonyddol, llyfn a llinol wedi’i bwysoli.
Cynigir ymgyfarwyddo â’u pwrpas:

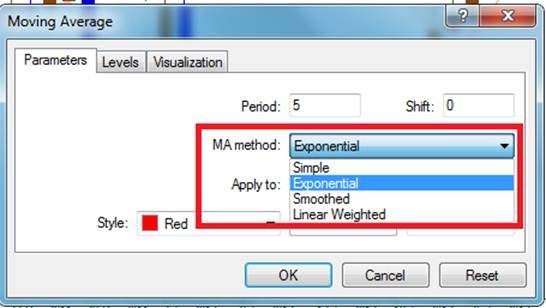
1. Y Cyfartaledd Symud Syml yw swm prisiau cau’r offeryn a ddewiswyd, sy’n cynrychioli sawl cyfnod. Ar ben hynny, mae’r dangosydd hwn wedi’i rannu â nifer y cyfnodau hyn. Nid trwy hap a damwain y galwyd y dangosydd yn syml, mae’n hawdd ei ddefnyddio ac fe’i hystyrir yn sylfaenol.
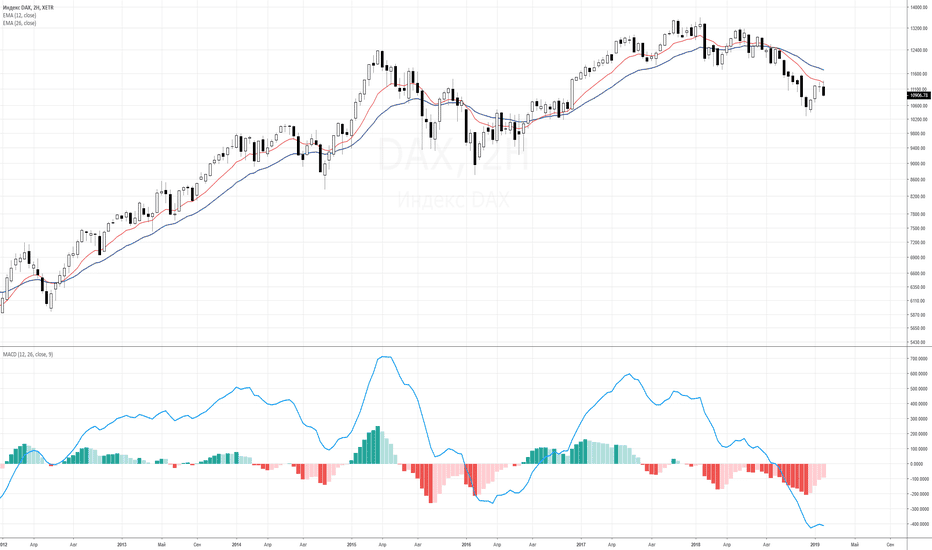
2. Cyfartaledd Symud Esbonyddol – yn yr achos hwn, mae rhan o’r pris cau gwirioneddol yn cael ei ychwanegu at werth blaenorol y cyfartaledd symudol.
3. Y Cyfartaledd Symud Llinol Pwysoledig yw dangosydd mwyaf gweithredol y teulu. Gall y math hwn roi nifer fawr o signalau ffug, ond mae’n gyflymach nag eraill i nodi newidiadau yn y pris. Anaml y bydd masnachwyr yn defnyddio’r dangosydd hwn.
4. Y Cyfartaledd Symud Llyfn yw’r llyfnaf ymhlith y lleill. Mae SMMA yn darparu dull cyfrifo sydd, yn wahanol i SMA, hefyd yn ystyried gwerthoedd hen ffasiwn. Gyda llaw, yn ymarferol, anaml iawn y defnyddir y cyfartaledd symud llyfn.

Cyfartaledd symudol esbonyddol – sut i sefydlu a sut i’w ddefnyddio’n ymarferol: https://youtu.be/3-4CwYfphXc

Cymhwysiad ymarferol – algorithm sut i ddefnyddio cyfartaledd symudol

Mae’r cyfartaledd symudol yn ddangosydd tuedd, yn hyn o beth, mae strategaethau masnachu yn seiliedig arno yn eithaf perthnasol. Mae 3 prif ffordd o ddefnyddio signalau:

1. Cyfeiriad cyffredinol . Yn cynrychioli’r mesurau tueddiadau gwirioneddol. Gall fod yn dymor byr, canolig neu hir. Yn yr achos hwn, mae MA yn cael ei gyfeirio i fyny mewn uptrend, ac i lawr mewn dirywiad. Mae modd arall – fflat, pan fo’r cyfartaledd symudol yn llorweddol.

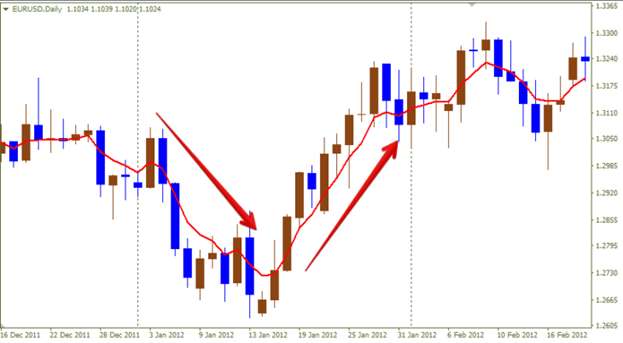
2. Croesi cyfartaleddau symudol gyda chyfnodau gwahanol . Mae lefel y signal bob amser yn dibynnu ar yr MA gyda’r cyfnod lleiaf. Os oes croesfan yn y llinell nesaf (o’r gwaelod i’r brig), yna arwydd ar gyfer caffael ased. Fel arall, mae’n signal gwerthu.
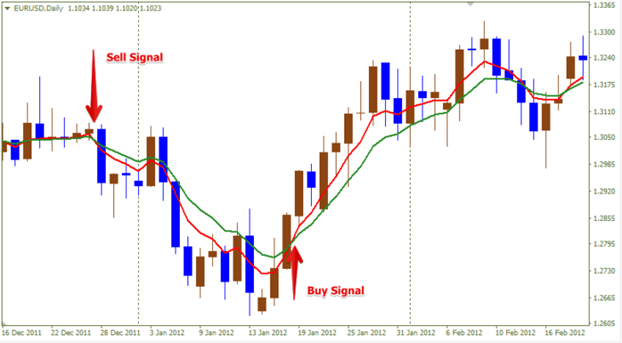
3. Cefnogaeth a gwrthiant . Mae croestoriad y llinell yn fath o signal i gyfeiriad y groesffordd ei hun. Mae’r dangosydd ar gyfer ased penodol yn hollol wahanol. Argymhellir cofio hyn.

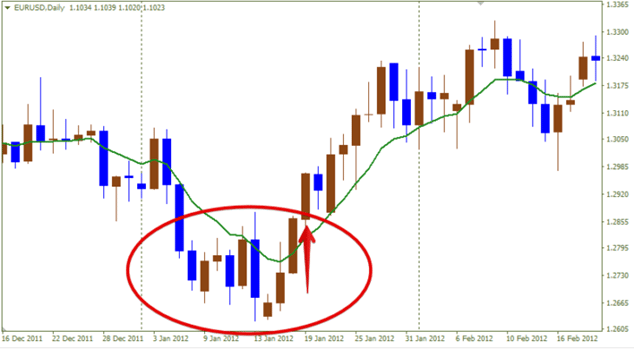
Penderfynu ar duedd trwy symud

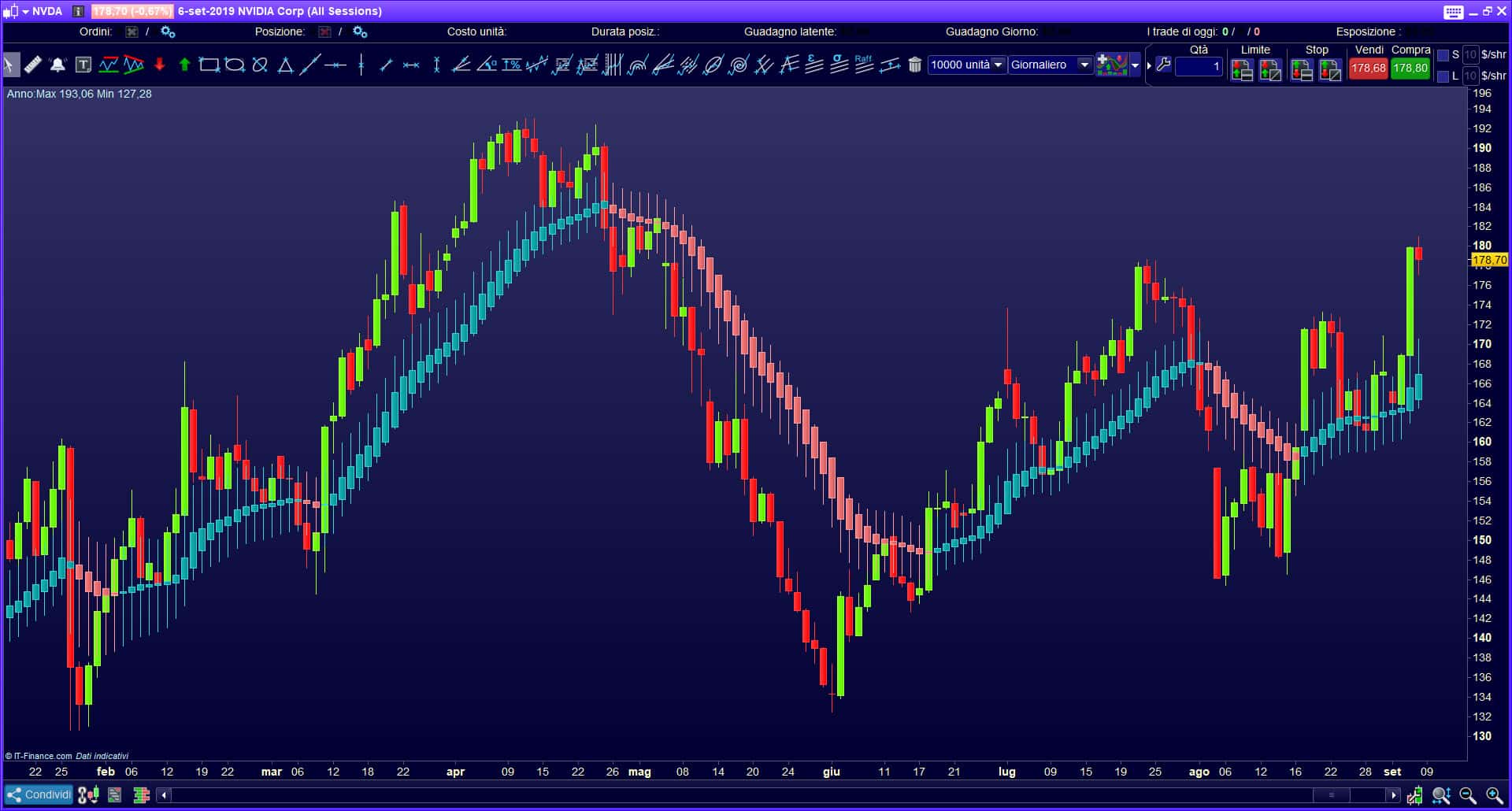
Mae’r cyfartaledd symudol yn dangos cyfeiriad y duedd. Os bydd y dangosydd pris wedi’i leoli uwchben y llinell, sy’n cael ei droi i fyny, yna mae’r duedd ar i fyny. Pan fydd 3 cyfartaledd symudol yn troi’n llinellau cyfochrog ac yn “edrych” i gyfeiriad penodol, yna dyma’r signal cryfaf. Ar yr un pryd, dylent gael cyfnodau gwahanol. Os bydd y pris yn symud mewn ystod benodol ar y farchnad (nid ar hyd un taflwybr), yna mae’n bosibl y bydd nifer fawr o signalau ychwanegol.

croesi cyfartalog symud

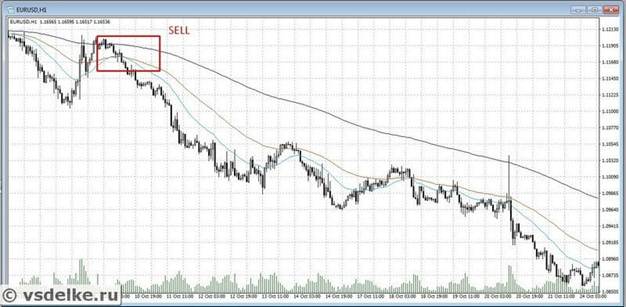
Pan fydd y cyfartaledd sy’n symud yn gyflym yn croesi’r un araf, o’r gwaelod i fyny, mae signal eithaf cryf i brynu (Prynu) yn debygol. Os caiff y sefyllfa ei gwrthdroi (o’r brig i’r gwaelod), yna mae hwn yn arwydd i’w werthu (Gwerthu). Ond os nad oes tueddiad pwrpasol yn y farchnad fuddsoddi, yna mae yna lawer o signalau gwag na fyddant yn dod â’r buddion disgwyliedig.

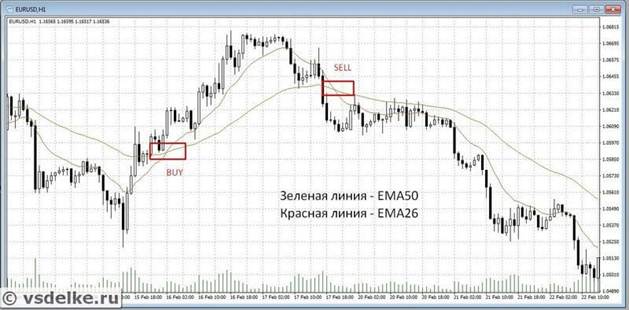
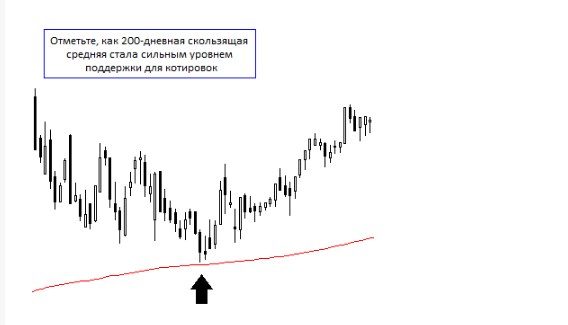
Pennu lefelau ymwrthedd a chefnogaeth

Wrth ffurfio’r lefelau hyn, efallai y bydd y pris yn symud i ffwrdd o’r cyfartaledd symudol. Mae hyn yn digwydd yn fwy amlwg yn achos cyfartaledd symudol esbonyddol gyda chyfnodau sylweddol. Ar hyn o bryd, mae’n fwyaf manteisiol i fynd i mewn i sefyllfa.

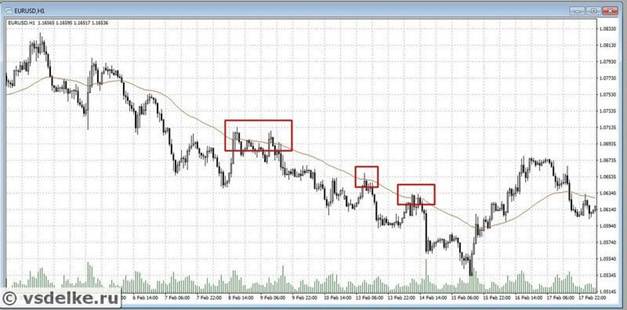
Tri chyfartaledd symudol yn gyfochrog â’i gilydd

Fel arfer maent yn cael eu hadeiladu bron yn gyfochrog â’i gilydd. Mae hwn yn gyfle da iawn i fynd i mewn i uchder tuedd. Os yw’r weithred ar y cychwyn cyntaf yn cael ei darlunio ar y siart, yna yn iaith amodol masnachwyr, gellir ei ddisgrifio fel “ceg agored aligator”.

Fformiwlâu ar gyfer cyfrifo pob math o gyfartaleddau symudol

Ar ôl dod yn gyfarwydd â phob math o gyfartaledd symudol mewn masnachu, argymhellir astudio eu fformiwlâu cyfrifo.

Fformiwla SMA

Er mwyn darganfod dangosydd cyfartaledd symudol syml, mae’n ddigon cymhwyso’r fformiwla ganlynol:
SMA \u003d SUM (CLOSE (i), N) / N
Eglurhad:

• SWM yw’r swm;
• Mae CAU (i) yn golygu pris y cyfnod a gyflwynir;
• N yw nifer y cyfnodau.

Mae SMA wedi’i gynllunio i gydbwyso prisiau amserlen benodol. Mae disgyrchiant penodol unrhyw werth dilynol wedi’i osod i’r un peth. Yn achos neidiau pris diriaethol, bydd SMA yn eu cymryd i ystyriaeth ynghyd â’r duedd pris safonol.

Fformiwla Cyfrifo LCA

I gyfrifo’r cyfartaledd symudol esbonyddol, mae angen i chi ysgrifennu’r fformiwla fel a ganlyn:
EMA = (CAU (i) * P) + (EMA (i – 1) * (100 – P))
Eglurhad:

• CAU (i) – dangosydd pris y cyfnod penodol;
• LCA (i – 1) – gradd y LCA ar gyfer y cyfnod blaenorol;
• Mae P yn rhan benodol o’r gwerth pris.

LCA yw’r math o gyfartaledd symudol a ddefnyddir amlaf wrth fasnachu. Gyda’i help, mae’n bosibl dileu diffygion SMA. Yn yr achos hwn, mae’n troi allan i ddarganfod union sefyllfa’r farchnad mewn cyfnod penodol. A hefyd y dangosydd DEMA – EMA dwbl: https://articles.opexflow.com/analysis-methods-and-tools/indikator-dema.htm

Fformiwla Cyfrifo SMMA

I gyfrifo’r cyfartaledd symud llyfn, gallwch ddefnyddio’r fformiwla ganlynol:
SMMA (i) = (SMMA (i – 1) * (N – 1) + CAU (i)) / N
Eglurhad:

• SMMA (i – 1) – dangosydd y gannwyll flaenorol;
• CAU (i) – pris cau cyfredol;
• N yw gradd y cyfnod llyfnu.

Fformiwla Gyfrifo LWMA

Wrth gyfrifo cyfartaledd symudol wedi’i bwysoli’n llinol, mae angen i chi gael eich arwain gan y fformiwla ganlynol:
LWMA = SUM (CAU (i) * i, N) / SUM (i, N)
Eglurhad:

• SUM – dangosydd swm;
• CAU(i) – pris cau gwirioneddol;
• SUM (i, N) yw swm y cyfernodau.
• N yw dynodiad y cyfnod.

Diolch i gyfartaleddau symudol wedi’u pwysoli’n llinol a’u llyfnu, mae’n bosibl cysoni arwyddocâd prisiau am gyfnod cyfrifo penodol.

Nodweddion gosod cyfnodau

Gellir ffurfweddu paramedrau dangosydd yn unol â dymuniadau’r defnyddiwr. Gall osod cyfwng amser cyfleus. Po leiaf ydyw, y mwyaf sensitif a chywir yw’r cyfartaledd symudol mewn signalau. Er gwaethaf safbwyntiau amrywiol, nid oes unrhyw egwyl amser “cywir”. I osod yr amserlen orau, bydd yn rhaid i’r defnyddiwr arbrofi am ychydig. O ganlyniad, bydd yn deall pa gyfnod sydd fwyaf optimaidd iddo, yn ôl ei strategaeth bersonol. Cyfartaleddau Symud yn TradingView:

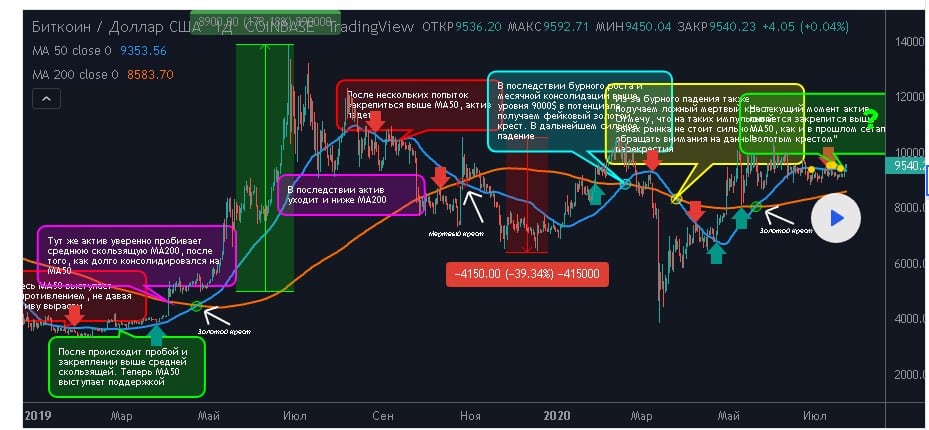
Cyfartaleddau symudol ar gyfer croen y pen

Mae “Scalping” yn cael ei ystyried yn derm bratiaith wrth fasnachu. Strategaethau masnachu tymor byr a elwir felly. Mae cyfartaleddau symudol mewn scalping yn cael eu gwahaniaethu trwy weithredu nifer fawr o drafodion. Mae’r dull hwn yn addas ar gyfer y rhai nad ydynt yn dilyn nodau byd-eang o ran elw. Mewn masnachu scalping, defnyddir siartiau gydag amserlenni bach yn aml. Mae’r strategaeth hon yn ddigon hen yn gyffredin, yn ddiweddar. Roedd hyn oherwydd y defnydd o fasnachu ymyl. Mae’r dull hwn yn effeithiol iawn a gall ddod â chanlyniadau ariannol da. Mae calping yn gyfleus i fasnachwyr sy’n buddsoddi adneuon bach ac yn stopio ar gydweithrediad tymor byr. Ond nid yw hyn yn golygu bod y strategaeth yn syml ac yn llai ynni-ddwys. Bydd yn rhaid i’r defnyddiwr neilltuo llawer o amser i gyflawni incwm uchel. Mae angen edrych ar y farchnad ariannol yn ystod y dydd yn rheolaidd er mwyn dod o hyd i signal masnachu, yn ogystal â chefnogi trafodion agored. Diolch i scalping, bydd masnachwr yn gallu denu incwm da. Y prif beth yw profi’r system fasnachu yn ymarferol, peidio â bod ofn arbrofion, neilltuo digon o amser i gynnal trafodion a’i wneud yn systematig. Dangosydd cyfartalog symudol – terfynell fasnachu QUIK: https://youtu.be/ZOUMHFmpruk

Nodweddion masnachu ar gyfartaleddau symudol, gydag enghreifftiau

Mae yna lawer o strategaethau masnachu gan ddefnyddio cyfartaleddau symudol. Yn eu plith, mae’n werth tynnu sylw at 4 prif amrywiad ar gyfer masnachu:

1. MA yn croesi yn ôl pris;
2. dadansoddiad o 2 neu fwy o gyfartaleddau symudol;
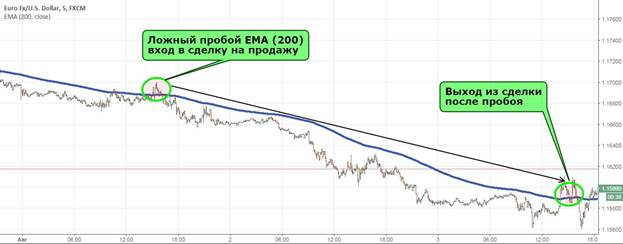
3. croesi ffug MA;
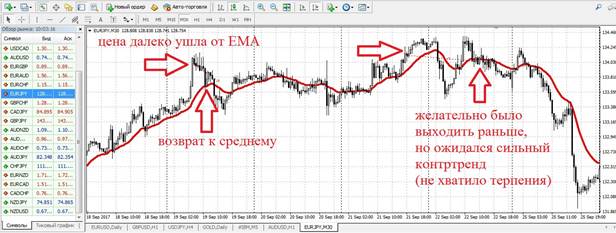
4. dychwelyd i’r cyfartaledd.

Weithiau mae cyfuniadau o rai dangosyddion ag eraill yn cael eu ffurfio. Bwriedir ystyried pob un o’r achosion yn fwy manwl. Ystyrir mai croesi’r SMA gan y pris yw’r strategaeth symlaf y gall unrhyw ddefnyddiwr ei chymhwyso, waeth beth fo lefel eu gwybodaeth yn y maes buddsoddi. O ran y farchnad Forex, ni fydd strategaeth o’r fath yn effeithiol. Os yw’r SMA yn croesi o’r gwaelod i’r brig, bydd yn bosibl mynd i mewn i safle hir, fel arall (o’r brig i’r gwaelod), bydd cofnod byr yn cael ei wneud. I adael y fasnach, dylech aros am y toriad nesaf.
Mae torri allan o 2 neu fwy o gyfartaleddau symudol hefyd yn opsiwn hawdd. Ond nid yw’n arbennig o effeithiol. Mae’n digwydd fel hyn: LCA (1) yn torri LCA (2) o’r top i’r gwaelod. Yn ôl y gyfatebiaeth arall, mae’n bosibl nodi’n fyr. Felly, os yw’r groesffordd yn mynd o’r gwaelod i’r brig, yna bydd cofnod hir yn cael ei wneud. Ar y toriad nesaf, mae’r fasnach yn gadael.
Cyfeirir hefyd at y gorgyffwrdd ffug MA fel y “strategaeth torri allan ffug”. Mae’n ymddangos ar ôl croesi’r LCA. Ar ôl peth amser (y prif beth yw aros amdano), bydd y pris yn dychwelyd. Cyn gynted ag y bydd hyn yn digwydd, gallwch chi fynd i mewn i’r trafodiad yn ddiogel. Felly, rhaid gadael allan ohono ar ôl croesi nesaf yr LCA.
Dychwelyd i’r cyfartaledd yw un o’r defnyddiau mwyaf annodweddiadol o’r offeryn cyfartaledd symudol wrth fasnachu. Mae masnachu yn seiliedig ar rifersiynau i’r cyfartaledd. Hynny yw, mae angen gwneud cofnod yn erbyn y duedd (mae hyn yn bwysig). Yn ystod y cyfnod hwn, bydd y pris yn mynd ymhell o’r cyfartaledd symudol esbonyddol. Dylech adael pan fyddwch yn llwyddo i gyrraedd dangosydd pris LCA (21). Er, os gwnewch hynny 3-4 pwynt yn gynharach, ni fydd y newidiadau yn arwyddocaol.
Sut mae Masnachwyr yn Defnyddio’r Cyfartaledd Symudol mewn Masnachu – Algorithmau a Strategaeth: https://youtu.be/WrtMA-SLw9g

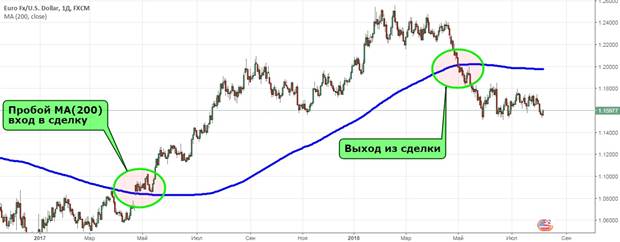
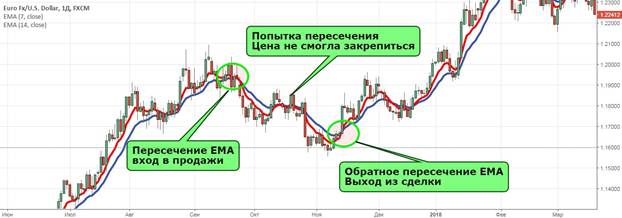
Detholiad cywir o’r cyfnod ar gyfer masnachu ar gyfartaledd symudol

Yn aml mae gan fasnachwyr cyntaf ddiddordeb yn y ffordd orau i ddewis cyfnod ar gyfer masnachu. Mewn gwirionedd, nid oes dim byd cymhleth, y prif beth yw deall gwirioneddau syml. Er enghraifft, y cyfnod cyfartalog symudol yw nifer y canhwyllau ar yr amserlen. Mae cyfnod amser y cyfartaledd symudol yn dibynnu i raddau helaeth ar ba mor hir y gall y defnyddiwr ddal y fasnach. Er enghraifft, roedd yn bwriadu cadw’r fargen am tua 1 awr. Yn yr achos hwn, bydd y dangosydd (12) ar y siart 5 munud yn gwneud hynny. Yn amlwg, mae’r rhain yn brisiau cyfartalog am 1 awr. Gallwch chi actio ychydig yn wahanol. Tybiwch fod awydd i ddal swydd am 1-2 wythnos. Yn yr achos hwn, yn fwy nag erioed, bydd LCA (7) a (14) ar D1 yn gwneud hynny. Fodd bynnag, o ystyried y ffaith mai dim ond 5 diwrnod gwaith mewn wythnos (gan nad yw penwythnosau’n cael eu hystyried), mae’n fwy rhesymegol cymryd LCA (5) a (10).

Safle o gyfartaleddau symudol yn y farchnad stoc

Yn bendant mae lle i ehangu yma. Gan fod cyfartaleddau symudol yn bwysicach o lawer yn y farchnad stoc, mae’n werth deall y mater hwn yn drylwyr. Mae’r rheswm yn gorwedd yn y gwahaniaeth rhwng y farchnad Forex ac offerynnau cyfnewid nodweddiadol. Os byddwch yn ymchwilio i’r manylion, daw’n amlwg ar Forex y gall cymhareb economïau dwy wladwriaeth ar wahân fod yn hynod anrhagweladwy. Mae’r sefyllfa’n newid yn gyson. Felly, mae parau arian yn aml yn newid eu cyfeiriad yn ddramatig. Ar ben hynny, nid oes unrhyw duedd glir ar gyfer cynnydd cyson, neu i’r gwrthwyneb, ar gyfer gostyngiad sydyn. Cyn belled ag y mae’r farchnad stoc yn y cwestiwn, mae stociau a mynegeion ffyniannus yn cynyddu heb newidiadau sydyn, a hefyd yn dod hyd yn oed yn fwy rhagweladwy. Fodd bynnag, yn ystod cyfnodau o argyfwng, mae symudiadau a neidiau mawr sy’n anodd eu rhagweld ymlaen llaw. Felly, mae’n troi allan bod y farchnad stoc bron yn frand pur, gydag ychydig eithriadau. Mae hyn yn golygu y gallwch chi wneud arian da ar gyfartaleddau symudol os ydych chi’n cymryd y gweithgaredd hwn o ddifrif.
Mae’r mynegai bob amser mewn uptrend. Yn seiliedig ar hyn, gallwn ddod i’r casgliad bod y strategaeth hon yn hawdd iawn i’w defnyddio. Mae’n ddigon i brynu, tra bod y mynegai yn agos at y cyfartaledd symudol neu wedi gostwng ychydig. Ar ôl hynny, dylech gadw’r offeryn yn y portffolio nes ei fod yn uwch na’r cyfartaledd.
Yn ôl profion cyfartalog symudol esbonyddol, mae’n werth prynu ased pan fydd y pris yn uwch. Yn dilyn algorithm rhesymegol, mae’n well gadael masnach pan fydd y pris yn is.
Awgrymir rhoi sylw i’r canlyniadau diagnostig wrth gymhwyso LCA (200). Fel y gallwch weld, mae’r gostyngiad tua thair gwaith yn llai. Fodd bynnag, i raddau llai, mae’n effeithio ar incwm. Mae’n amlwg bod y lefel wedi newid ychydig.
Mae’r opsiwn yn gweithio, ond ni ddylech feddwl bod llwyddiant techneg fasnachu o’r fath yn berthnasol i’r holl stociau, asedau gwerthfawr a mynegeion. Mae yna hefyd rai sy’n symud yn anrhagweladwy iawn. Er bod analytics ei greu ar gyfer achosion o’r fath. Bydd gwiriad trylwyr o hanes dyfyniadau hefyd yn helpu. Os byddwn, er enghraifft, yn cymryd marchnad stoc Ffederasiwn Rwseg, yna gallwn weld yn y realiti hwn ei bod yn llawer anoddach gweithio gyda chyfartaleddau symudol.
Bydd incwm ar y farchnad stoc Rwseg yn gallu cael ar y dychwelyd i’r gwerthoedd cyfartalog. Mae hyn oherwydd y ffaith bod y farchnad yn aml wedi’i lleoli mewn sianel eang. Boed hynny ag y bo modd, yn y farchnad stoc cyflawnir y nod hwn yn gymharol gyflymach ac yn haws nag mewn masnachu Forex. Y prif beth yw gweithio’n galed ar y dewis o offerynnau sefydlog, boed yn fynegeion Americanaidd, cyfrannau o fentrau mawr, dogfennaeth werthfawr o frandiau enwog, ac ati. Cyn buddsoddi ar hap, mae’n well ceisio defnyddio cyfartaleddau symudol, rhesymoli’r incwm a dderbynnir a lleihau’r tynnu i lawr. Dyma sut rydych chi’n cael canlyniadau gwych.