Ko te raupapa Fibonacci he raupapa tau ko ia waahanga e whai ake nei ko te tapeke o nga mea e rua o mua:
1,1,2,3,5,8,13,21,34,55,89, … E hono ana enei whika na te maha o nga hononga whakamere. Ko ia tau he 1.618 nga wa o te tau o mua. Ko ia keehi ka rite ki te 0.618 o enei e whai ake nei. 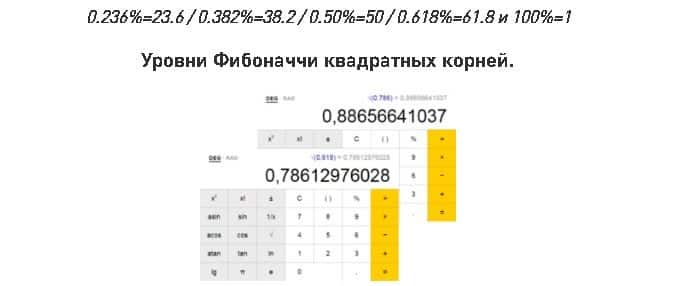
Ka puta mai i te wa e tirotirohia ana te maakete, he maha nga taumata e whakamahia ana: 0.0%, 23.6%, 38.2%, 50.0%, 61.8%, 76.4%, 100.0%, 161.8% , 261.8% me 423.6%, te tino kaha. o e 61.%.
He tino mohio enei tau ahua noa, a kia kite tatou me pehea te whakamahi. Ko nga tauira Fibonacci he pai te whakamahi i te taha o etahi atu tauira me nga tohu. He maha nga wa e tohu ana ratou ki te huarahi whanui ake. Ko te toronga Fibonacci ka hoatu ki a koe he whaainga utu motuhake, engari kaore he tikanga mena ka mohio koe ka pakaru pea. Ko te whakamatautau whakatau tata utu Fibonacci e hiahia ana ki te tauira tapatoru, te whakapumautanga rōrahi, me te aromatawai i te ahua katoa. Ma te whakakotahi i nga tohu me nga mahere me te maha o nga taputapu Fibonacci e waatea ana, ka taea e koe te whakanui ake i to tupono ki te hokohoko angitu. Kia mahara kaore he ine kotahi e whakaatu ana he tino tika nga mea katoa (mehemea kei reira, ka whai rawa tatou katoa). Heoi, ka tohu te maha o nga tohu ki te huarahi kotahi, ka taea e koe te whai whakaaro pai mo te waahi kei te haere te utu. [caption id=”attachment_306″
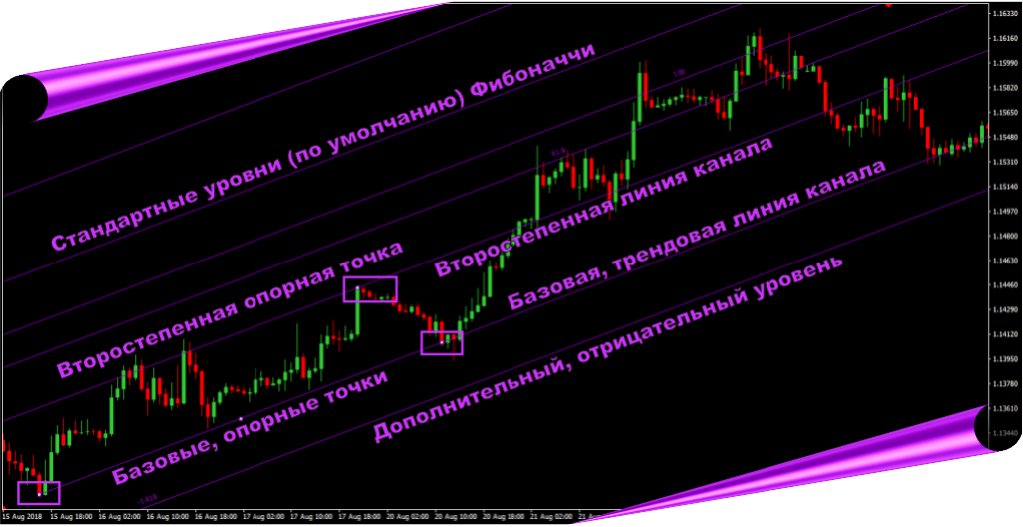
- te whakatau i te wa mo te whakatikatika utu me te whakakotahi;
- te tohu i te wa e huri ana te ahua katoa;
- te arotake i nga wa tino pai mo te whakatuwhera i nga ota;
He ngawari tenei tohu ki te whakamahi, engari ka taea te whakapai ake i te tika o tetahi punaha hokohoko.
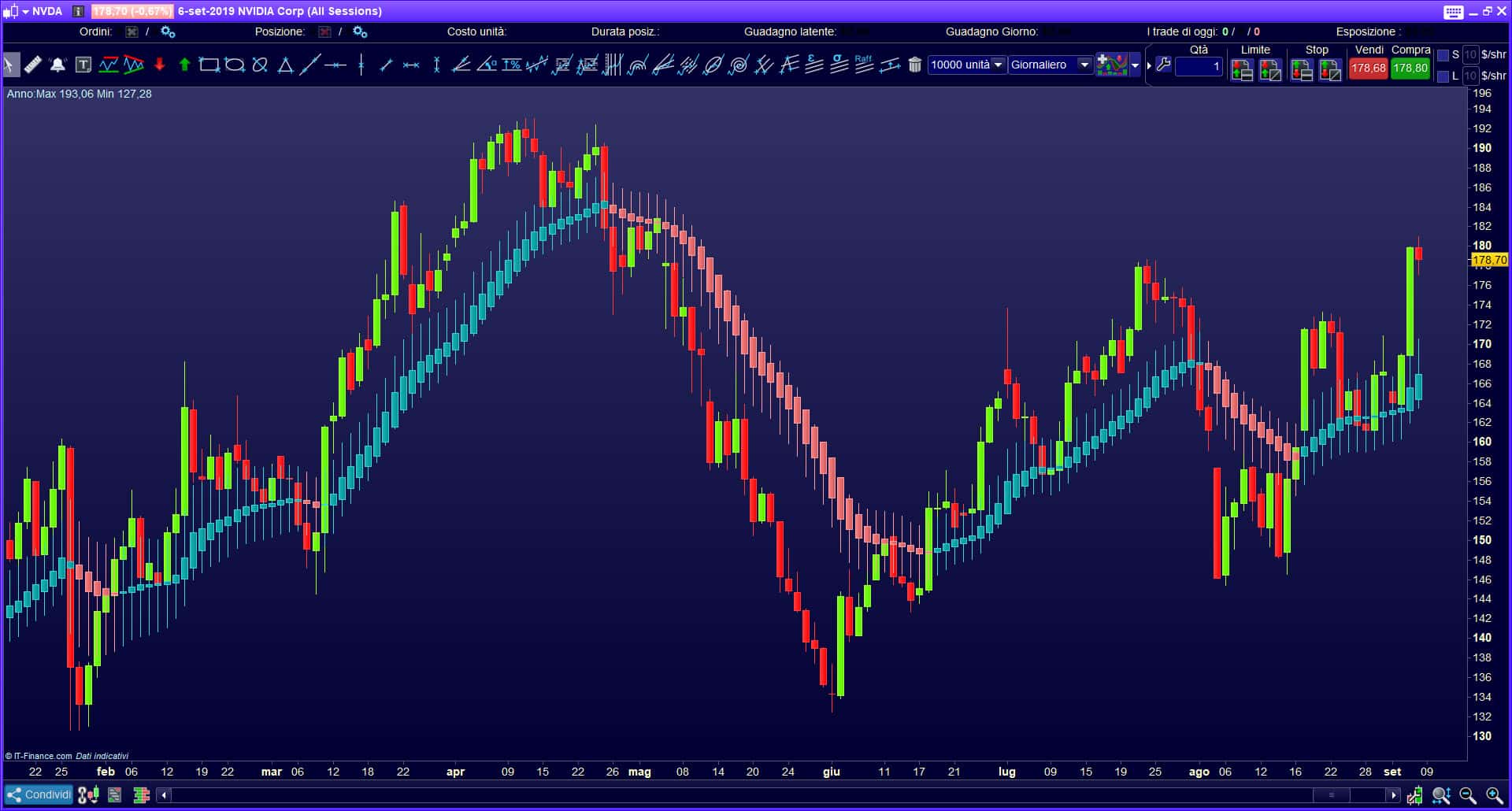
Me pehea te hanga hongere Fibonacci i roto i te tauranga me o koe ake?
Hei waihanga i nga waahana Fibonacci ki te tauranga MetaTrader4, tohua: “Whakauru” – “Wairangi” – “Fibonacci”: [caption id="attachment_308" align="aligncenter" width="509"]
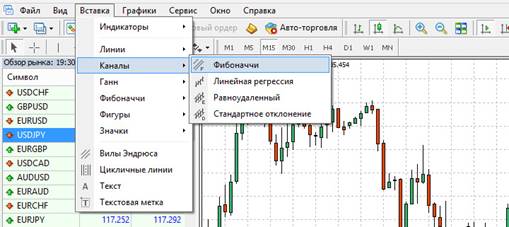
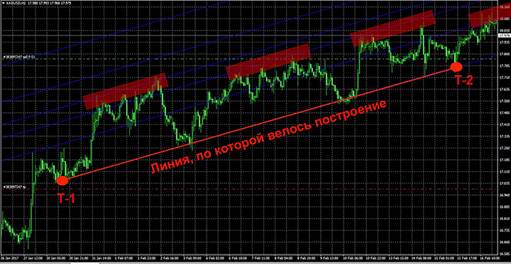
Me pehea te whakamahi i nga Channels Fibonacci?
He rereke nga rautaki mo te whakamahi i te hongere, ka iti ake te morearea ki te hoko ota i runga i te ahua o naianei ka peke atu te raarangi i te raina ka oti katoa te hanga. Me kati te ota ina tae te utu ki te taumata, a, kei reira nga tohu o tona hokinga tere. He aha te whakamahi i te tohu hangarau mai i te roopu oscillators, i te rautaki Utu Mahi kaore he tohu? He pai ake te whiringa whakamutunga na te mea ka nui ake te tika. I runga i te rautaki whakamahinga, kaore nga waahana e rereke mai i nga taumata Fibonacci, engari ka taea te whakamahi mo nga nekehanga o te ao me te nui o te rereketanga. Ko te tino o te taputapu tātari hangarau Fibonacci hongere – te hanga, te whakamaoritanga o nga hua, te whakamahi mahi i roto i te hokohoko: https://youtu.be/izX0GDoupGA
Te rautaki a te kaituhi mo te whakamahi i te hongere Fibonacci
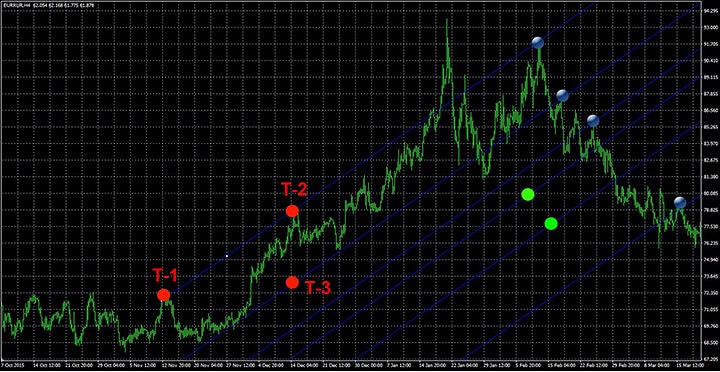
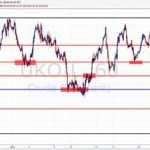
Ko tetahi o nga rautaki mo te whakamahi i te waahana Fibonacci ko te whakamatautau i ona tohu kaore i te wa tonu, engari ma te whakarereke i te ahunga o te nekehanga utu. Mena kei te piki ake te rawa, kaore te hongere Fib e totoro teitei ake (penei i te taha o runga ake nei), engari kei raro iho, me te mea kei te heke. I tenei keehi, ka whakahaerehia te hanga i runga i nga uara tino nui o te nekehanga utu, e hanga ana i nga “tahataha” e whakaiti ana i te hanga o te tūtohi. Ka pakaru nga raina hanga, ka whiwhi nga taumata nekehanga hei whakaū i te huringa o te ahunga me te whakatau i te wa tika o nga whakahau whakatuwhera:
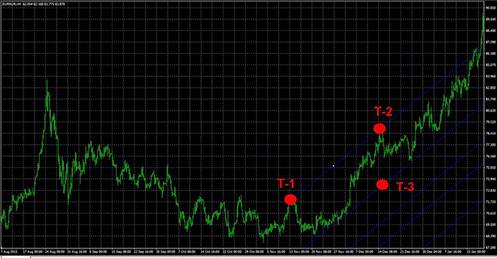
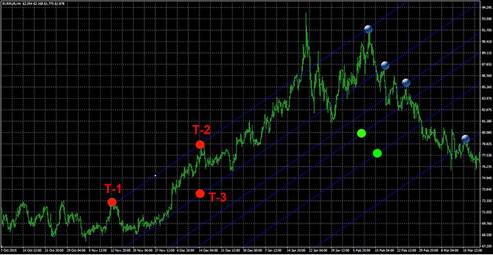
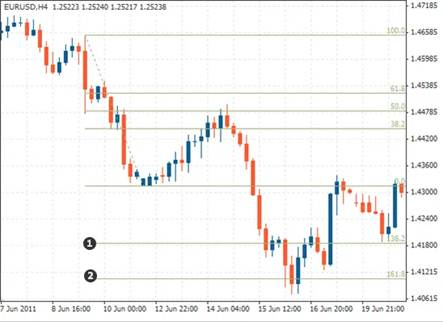
Ko te hongere tika he hongere kua whakaritea i runga i nga waahi iti e rua me nga waahi teitei e rua. Heoi, i roto i te mahi he maha nga wa i muri i tana whakapumautanga, ka huri te huarahi i te huarahi.
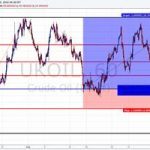
Kia whakamatautauhia te matapae nekehanga utu i te waahana e heke mai nei. Ko nga taumata Fibonacci ka awhina i a maatau i konei.
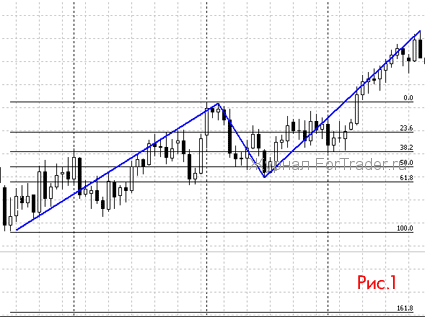
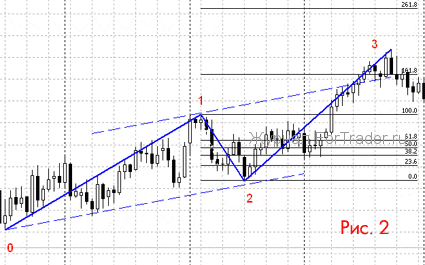
Nga taumata whakatika i runga i te Fibonacci
Koinei te whakamahinga ngawari o nga tau Fibonacci. Ko enei i runga i te meka ka taea te wehewehe i te ahua ki nga waahanga 6, a ka whai waahi tetahi waahanga. Ki te hanga i te matiti Fibonacci (i etahi wa ka kiia ko nga taumata), me rapu e koe he ahua maamaa ake, heke iho ranei, ka toia te matiti mai i te timatanga ki te mutunga.
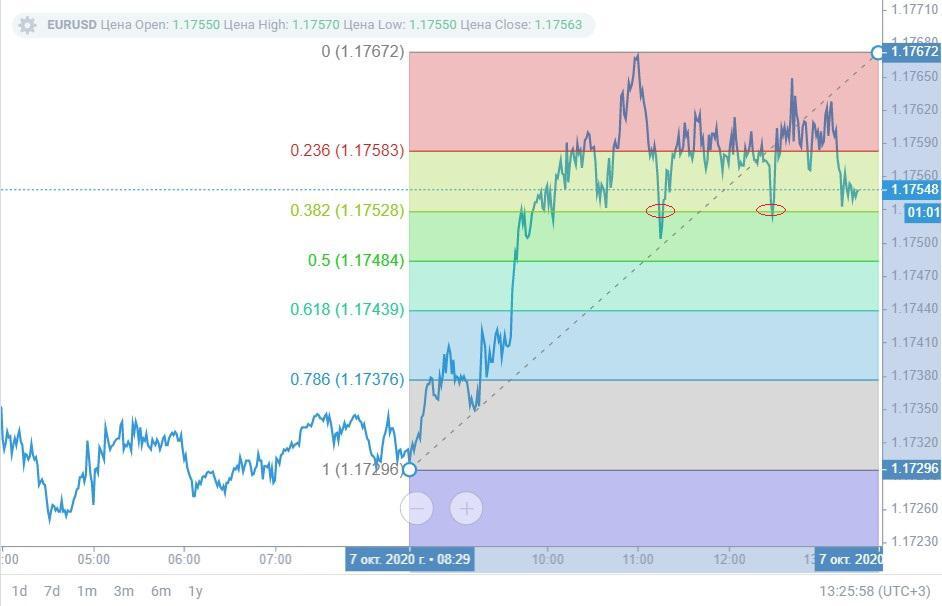
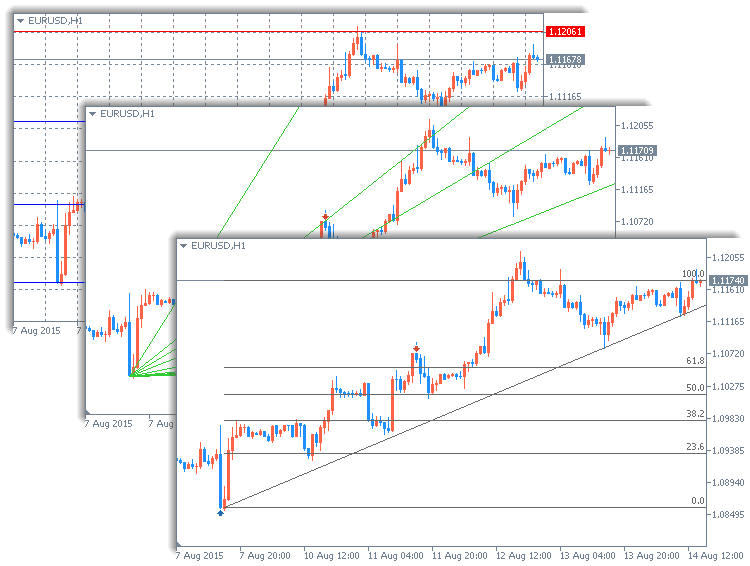
Te pai me te kino o te taputapu Fibonacci
Ko nga painga matua o te tohu ko te kaha ki te:
- matapae i nga whaainga hua me te aukati tika i nga mate;
- te mahi wawe i nga ota tarewa;
- te whakamahi i nga rautaki au me te aukati i te ahua;
- mahi i nga wa katoa, i waenganui o te ra me nga wa roa.
Ko nga tino kino o te tohu:
- kaore e pai mo te TF iti;
- he uaua ake te hanga i nga rautaki algorithmic e ai ki a Fibonacci i runga i etahi atu tohu. Na tenei, he uaua ake te whakamatautau i te maha o nga taputapu kia kitea ai nga tohu Fibonacci pono i roto i te hokohoko;
- he uaua ki te whakatau i te timatanga (te timatanga o te ia);
- te koretake o te tohu i runga i nga papa.
I muri i te tātari i nga pai me nga huakore katoa, ka taea e tatou te whakatau ka taea te whakamahi a Fibonacci hei tikanga taapiri hei whakatau i o tatou tuunga, engari hei taapiri noa. Kaua e hoko, hoko atu ranei i te 50%, 61.8% i runga i te matapōkere me te tumanako ki nga hua pai mo te wa roa – he tino uaua nga maakete ki te arahi i tetahi uara Fibonacci.